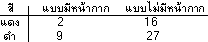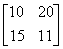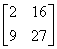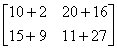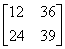เมทริกซ์
เมทริกซ์ (Matrix) คือ กลุ่มของสมาชิกที่เรียงในแนวนอนเรียกว่า แถว
และเรียงในแถวตั้งเรียกว่า หลัก เป็นรูปสี่เหลี่ยมมุมฉาก
สมาชิกทั้งหมดอยู่ภายในวงเล็บ [ ] หรือ ( )
และสมาชิกของเมทริกซ์ที่เขียนเป็นแนวนอนเรียกว่า สมาชิกที่อยู่ในแถว (Row) ของเมทริกซ์
สมาชิกของเมทริกซ์ที่เขียนเป็นแนวตั้งหรือแนวดิ่ง เรียกว่าสมาชิกที่อยู่ในหลัก (Column)
ของเมทริกซ์
7.1 ความหมายและชนิดของเมทริกซ์
เมทริกซ์ หมายถึง กลุ่มของจำนวนจริงที่นำมาจัดเรียนงกันให้เป็นแถว
แต่ละแถวมีจำนวนที่เท่าๆกัน โดยมีวงเล็บเล็ก ( ) หรือวงเลบ็บ [ ] ปิดล้อมไว้ เช่น
โดยทั่วไปแล้วเรามักนิยมใช้อักษร A , B , C , ... แทนเมทริกซ์
และใช้ตัวอักษรพิมพ์เล็ก a , b , c , ... แทนสมาชิกของเมทริกซ์
แต่ถ้าสมาชิกของเมทริกซ์มีจำนวนมาก
เราจะใช้อักษรเพียงตัวเดียวแทนสมาชิกและเขียนจำนวนต่อท้ายตัวอักษรดังกล่าวเพื่อบอกตำแหน่ง
ในระดับที่ต่ำลงไปเล็กน้อย เช่น
จำนวนที่เขียนตามหลังตัวอักษรนั้นจำทำหน้าที่บ่งบอกถึงตำแหน่งของสมาชิก เช่น
 เป็นสมาชิกในตำแหน่ง
แถวที่ 1 หลักที่ 1
เป็นสมาชิกในตำแหน่ง
แถวที่ 1 หลักที่ 1 เป็นสมาชิกในตำแหน่ง
แถวที่ 3 หลักที่ 1
เป็นสมาชิกในตำแหน่ง
แถวที่ 3 หลักที่ 1 เป็นสมาชิกในตำแหน่ง
แถวที่ 3 หลักที่ 3
เป็นสมาชิกในตำแหน่ง
แถวที่ 3 หลักที่ 3สรุป
 หมายถึง
สมาชิกในตำแหน่ง แถวที่ i หลักที่ j พูดกันแบบง่ายก็คือ
ตัวเลขตัวหน้า คือ แถว ตัวหลัง คือ หลัก นั่นเอง
หมายถึง
สมาชิกในตำแหน่ง แถวที่ i หลักที่ j พูดกันแบบง่ายก็คือ
ตัวเลขตัวหน้า คือ แถว ตัวหลัง คือ หลัก นั่นเอง
แต่ในการเขียนเช่นนี้ค่อนข้างยืดยาว
เราจึงนิยมใช้เขียนเป็น
 แทน โดยที่ i
(แถว)
= 1 , 2 , 3 , .... , m
แทน โดยที่ i
(แถว)
= 1 , 2 , 3 , .... , m
j (หลัก) = 1 , 2 , 3 , .... , n
หรืออาจจะเขียนให้สั้นกว่านี้ได้อีกดังนี้ ดังนั้น
ถ้านักเรียนเห็นสัญลักษณ์นี้ ต้องทราบทันที่ว่า เมทริกซ์ A มีมิติ
ดังนั้น
ถ้านักเรียนเห็นสัญลักษณ์นี้ ต้องทราบทันที่ว่า เมทริกซ์ A มีมิติ  และมี
และมี  เป็นตัวแทนของสมาชิกโดยทั่วไป
เป็นตัวแทนของสมาชิกโดยทั่วไป
 แทน โดยที่ i
(แถว)
= 1 , 2 , 3 , .... , m
แทน โดยที่ i
(แถว)
= 1 , 2 , 3 , .... , mj (หลัก) = 1 , 2 , 3 , .... , n
หรืออาจจะเขียนให้สั้นกว่านี้ได้อีกดังนี้
 ดังนั้น
ถ้านักเรียนเห็นสัญลักษณ์นี้ ต้องทราบทันที่ว่า เมทริกซ์ A มีมิติ
ดังนั้น
ถ้านักเรียนเห็นสัญลักษณ์นี้ ต้องทราบทันที่ว่า เมทริกซ์ A มีมิติ  และมี
และมี  เป็นตัวแทนของสมาชิกโดยทั่วไป
เป็นตัวแทนของสมาชิกโดยทั่วไป
แต่ละจำนวนที่ประกอบขึ้นเป็นเมทริกซ์เรียกว่า สมาชิก (Elements)
ของเมทริกซ์
กำหนดให้ a เป็นเมทริกซ์ใดๆ ตำแหน่งสมาชิกของเมทริกซ์ a
มิติ
ถ้าเมทริกซ์ M1M1 มีสมาชิก mm แถว
และ nn หลัก
เราเรียกเมทริกซ์นั้นว่า เมทริกซ์ M1M1 มีมิติ m×nm×n หรือเรียกว่า เมทริกซ์ M1M1 มีขนาด m×nm×n
พิจารณาเมทริกซ์ M1,M2,M3M1,M2,M3 จากตัวอย่างข้างบนเราจะได้
เมทริกซ์ M1M1 มีมิติ 2×32×3
เมทริกซ์ M2M2 มีมิติ 3×23×2
เมทริกซ์ M3M3 มีมิติ 2×22×2
เมทริกซ์ M1M1 มีมิติ 2×32×3
เมทริกซ์ M2M2 มีมิติ 3×23×2
เมทริกซ์ M3M3 มีมิติ 2×22×2
7.2 ทรานสโพสของเมทริกซ์
ให้ Aเป็นเมทริกซ์มีมิติ m×nm×n เขียนแทนด้วย A=[aij]m×nA=[aij]m×n
ซึ่งทรานโพสของ Aเขียนแทนด้วย AtAt คือ
At=[aij]m×n=[aji]n×mAt=[aij]m×n=[aji]n×m
คือ เมทริกซ์ที่เกิดจากการนำสมาชิกในเมทริกซ์ AA สลับกันระหว่างแถวกับหลัก
ให้ A=[142536]A=[123456] และ B=⎡⎣⎢147258369⎤⎦⎥B=[123456789] ดังนั้น
At=⎡⎣⎢123456⎤⎦⎥At=[142536]
และ
Bt=⎡⎣⎢123456789⎤⎦⎥
7.3 การเท่ากันของเมทริกซ์
จากบทนิยาม เป็นการกำหนดว่า
เมทริกซ์สองเมทริกซ์จะเท่ากันได้ต้องประกอบด้วยเงื่อไข 2 ข้อ ดังนี้
(1) เมทริกซ์ทั้งสองต้องมีมิติเท่ากัน
(2) สมาชิกที่อยู่ในตำแหน่งเดียวกันต้องเท่ากัน
(1) เมทริกซ์ทั้งสองต้องมีมิติเท่ากัน
(2) สมาชิกที่อยู่ในตำแหน่งเดียวกันต้องเท่ากัน
ในตำแหน่งเดียวกันเท่ากันทุก ๆ ตำแหน่ง
7.4 การบวกและการลบเมทริกซ์
การบวกลบเมทริกซ์
ในการที่เมทริกซ์ตั้งแต่
2 เมทริกซ์ขึ้นไปจะนำมาบวกลบกันได้จะต้องมีมิติเดียวกัน
หลังจากนั้นให้นำสมาชิกที่อยู่ในตำแหน่งแถว และตำแหน่งสดมภ์ตรงกันมาบวกลบกันได้
ผลลัพธ์ที่ได้ใส่ไว้ที่ตำแหน่งแถว
และสดมภ์นั้นของเมทริกซ์ที่เก็บผลลัพธ์ของการบวกและลบ ซึ่งจะมีมิติเท่ากับมิติของเมทริกซ์ที่นำมาบวก
ลบกัน
ตัวอย่าง 1 แสดงถึงเมทริกซ์ใดที่สามารถบวก ลบกันได้
C = [7 8 9]
จะเห็นว่าเมทริกซ์ที่สามารถบวกลบกันได้นั้น
มีเมทริกซ์ A กับ C เท่านั้นเพราะว่าเมทริกซ์ A กับ C มีมิติเดียวกัน คือ 1x3 ซึ่งสัญลักษณ์สำหรับการบวก
ลบ คือ + -
ดังนั้น
ดังนั้น
A+C = [1 2
3] + [7 8 9]
A+C = [ 1+7 2+8 3+9 ]
A+C = [ 1+7 2+8 3+9 ]
สมาชิกที่อยู่ในตำแหน่งเดียวกัน สามารถ บวกกันได้เช่นสมาชิก 1,7 อยู่ในตำแหน่งเดียวกันคืออยู่ที่แถวที่ 1 และสดมภ์ที่ 1
=
[ 8 10 12 ]
A-C = [1 2
3] - [7 8 9]
A-C = [
1-7 2-8
3-9 ]
สมาชิกที่อยู่ในตำแหน่งเดียวกัน สามารถ ลบกันได้
= [ -6 -6 -6 ]
= [ -6 -6 -6 ]
จากการบวกลบเมทริกซ์ สามารถเขียนเป็นรูปทั่วไปของการบวกลบได้ดังนี้
ให้ A = [aij] และ B = [bij] ที่เป็นเมทริกซ์มิติ
mxn แล้วผลบวกของเมทริกซ์
A กับเมทริกซ์ B เป็น A+B ซึ่งมีค่าเป็น [aij + bij] มิติ mxn
ผลลบของเมทริกซ์ A กับเมทริกซ์ B
เป็น
A-B ซึ่งมีค่าเป็น [aij - bij]
มิติ mxn
ตัวอย่าง 2 บริษัทแห่งหนึ่งมี 2 สาขา จำหน่ายอะไหล่รถจักรยานยนต์ เช่นหมวกกันน๊อค
ซึ่งแต่ละสาขาได้แสดงข้อมูลของการจำหน่ายหมวกกันน๊อค เป็นจำนวนใบต่อวัน
แยกตามสีและแบบ ดังนี้
สาขาที่ 1
สาขาที่ 2
อยากทราบว่าจำหน่ายหมวกกันน๊อคทั้งหมดของทั้ง 2 สาขา แยกตาม สีและแบบจำนวนกี่ใบ
วิธีทำ
ดังนั้น
ทั้งสองเมทริกซ์
คำนวณหาค่าของผลรวมของเมทริกซ์ได้ดังนี้
จากผลลัพธ์ที่ได้นำมาแปลงกลับเป็นตารางได้ดังนี้
7.5 การคูณเมทริกซ์
การคูณเมทริกซ์
สรุปบลักษณะการคูณจำนวนจริงกับเมทริกซ์
ให้ a , b เป็นจำนวนจริง และ A , B เป็นเมทริกซ์ที่มีมิติ 
1. aA = Aa
2. (ab)A = a(bA) = b(aA)
3. a(A + B) = aA + aB
4. (a +b)A = aA + aB

1. aA = Aa
2. (ab)A = a(bA) = b(aA)
3. a(A + B) = aA + aB
4. (a +b)A = aA + aB
7.6 ดีเทอร์มิแนนต์ของเมทริกซ์
ดีเทอร์มิแนนท์ของเมตริกซ์ คือ
ค่าหรือตัวเลขที่ได้จากการปฏิบัติการภายในสมาชิกของ เมตริกซ์
ซึ่งจะเป็นเมทริกซ์จัตุรัสเท่านั้น คือ จำนวนแถว และหลักเท่ากัน ดีเทอร์มิแนนท์ของ
A จะเขียนแทนด้วยสัญลักษณ์ “det A” หรือ “|A|”
1. การหาดีเทอร์มิแนนท์ของเมทริกซ์ขนาด 1x1
ให้ A = [a11] จะได้ det(A) = a11
เช่น A = [5] จะได้ det A = 5
ให้ A=[aij]n×nA=[aij]n×n ซึ่งเราจะหา A−1A−1 จากสูตร
A−1=1detAadj(A)
A−1=1detAadj(A)
เมื่อ detA≠0ดังนั้น เราจึงสรุปได้ว่าถ้า ในจำนวนจริงนั้น 00 เป็นเพียงค่าเดียวที่ไม่มี เอกลักษณ์การคูณ ( ไม่มี 0−10−1)ส่วนในเมทริกซ์นั้นสมาชิกที่ไม่มีเอกลักษณ์การคูณ อาจมีได้หลายตัว (ทุก ๆ ตัวที่มีค่าดีเทอร์มีนัลต์เป็น 00)
เช่น [0000],[1212],[4836][0000],[1122],[4386] ล้วนแต่ไม่มีเอกลักษณ์การคูณทั้งสิ้น
เมื่อ detA≠0ดังนั้น เราจึงสรุปได้ว่าถ้า ในจำนวนจริงนั้น 00 เป็นเพียงค่าเดียวที่ไม่มี เอกลักษณ์การคูณ ( ไม่มี 0−10−1)ส่วนในเมทริกซ์นั้นสมาชิกที่ไม่มีเอกลักษณ์การคูณ อาจมีได้หลายตัว (ทุก ๆ ตัวที่มีค่าดีเทอร์มีนัลต์เป็น 00)
เช่น [0000],[1212],[4836][0000],[1122],[4386] ล้วนแต่ไม่มีเอกลักษณ์การคูณทั้งสิ้น
2. การหาดีเทอร์มิแนนท์ขนาด 2x2
ให้ A=[acbd]A=[abcd] ดีเทอร์มิแนนต์ของ AA ซึ่งเขียนแทนด้วย detAdetA และ |A||A|
detA=∣∣∣1324∣∣∣=(1)(4)−(3)(2)=−2detA=|1234|=(1)(4)−(3)(2)=−2
7.7 อินเวอร์สการคูณของเมทริกซ์
อินเวอร์สการคูณของเมทริกซ์
คงจำกันได้นะ อินเวอร์สการคูณของจำนวนจริง a คือ จำนวนจริงที่นำมาคูณกับจำนวนจริง a แล้วได้ผลเท่ากับเอกลักษณ์ 1 และเราใช้สัญลักษณ์ แทนอินเวอร์สการคูณของจำนวนจริง
a นั่นคือ
แทนอินเวอร์สการคูณของจำนวนจริง
a นั่นคือ 
ในทำนองเดียวกัน อินเวอร์สการคูณของเมทริกซ์ A ก็คือ เมทริกซ์ ซึ่งเมื่อนำมาคูณกับเมทริกซ์ A แล้วจะได้ผลลัพธ์เท่ากับเมทริกซ์เอกลักษณ์ I และเราใช้สัญลักษณ์ แทน อินเวอร์สการคูณของเมทริกซ์ นั่นคือ
แทน อินเวอร์สการคูณของเมทริกซ์ นั่นคือ 
แต่งเนื่องจาก กับ
กับ  นั้นต้องมีสมบัติการสลับที่สำหรับการคูณ
ซึ่งการที่จะเกิดลักษณะนี้ได้
นั้นต้องมีสมบัติการสลับที่สำหรับการคูณ
ซึ่งการที่จะเกิดลักษณะนี้ได้  และ
และ  ต้องเป็นเมทริกซ์ที่มีมิติเท่ากัน
ต้องเป็นเมทริกซ์ที่มีมิติเท่ากัน
คงจำกันได้นะ อินเวอร์สการคูณของจำนวนจริง a คือ จำนวนจริงที่นำมาคูณกับจำนวนจริง a แล้วได้ผลเท่ากับเอกลักษณ์ 1 และเราใช้สัญลักษณ์
 แทนอินเวอร์สการคูณของจำนวนจริง
a นั่นคือ
แทนอินเวอร์สการคูณของจำนวนจริง
a นั่นคือ 
ในทำนองเดียวกัน อินเวอร์สการคูณของเมทริกซ์ A ก็คือ เมทริกซ์ ซึ่งเมื่อนำมาคูณกับเมทริกซ์ A แล้วจะได้ผลลัพธ์เท่ากับเมทริกซ์เอกลักษณ์ I และเราใช้สัญลักษณ์
 แทน อินเวอร์สการคูณของเมทริกซ์ นั่นคือ
แทน อินเวอร์สการคูณของเมทริกซ์ นั่นคือ 
แต่งเนื่องจาก
 กับ
กับ  นั้นต้องมีสมบัติการสลับที่สำหรับการคูณ
ซึ่งการที่จะเกิดลักษณะนี้ได้
นั้นต้องมีสมบัติการสลับที่สำหรับการคูณ
ซึ่งการที่จะเกิดลักษณะนี้ได้  และ
และ  ต้องเป็นเมทริกซ์ที่มีมิติเท่ากัน
ต้องเป็นเมทริกซ์ที่มีมิติเท่ากัน
สรุป ถ้านักเรียนต้องการแสดงว่า
เมทริกซ์ B เป็นอินเวอร์สของเมทริกซ์ A นักเรียนต้องแสดงให้ได้ว่า AB = BA = I
7.8 การแก้ระบบสมการเชิงเส้นด้วยเมทริกซ์
การแก้ระบบสมการเชิงเส้นโดยวิธีนี้จะใช้ได้สะดวกที่สุดเมื่อระบบสมการเชิงเส้นมี 22 ตัวแปรแต่เมื่อระบบสมการเชิงเส้นของเรามีตัวแปรมากกว่า 33ตัวแปร
ในบางครั้งการแก้ระบบสมการโดยวิธีนี้ค่อนข้างจะยุ่งยากจึงไม่เป็นที่นิยม